2025. 1. 13. 13:33ㆍLLM(Large Language Model)의 기초/딥러닝
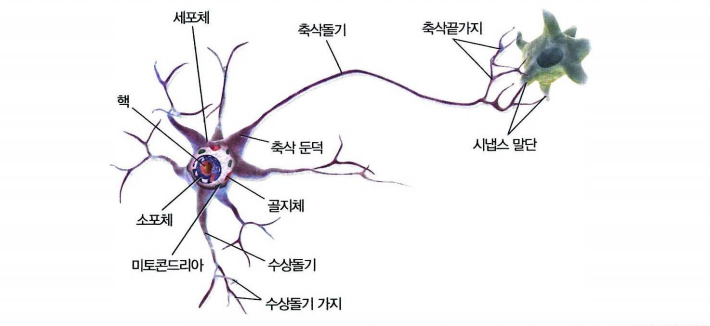
1.생물학적 뉴런
* 생물학적 뉴런은 신경계를 구성하는 기본 단위로, 정보를 수집, 처리, 전달하는 기능을 담당합니다.
* 뉴런은 크게 세 가지 주요 부분으로 나뉩니다: 수상돌기(dendrite), 세포체(cell body), 축삭(axon)입니다.
* 수상돌기는 다른 뉴런이나 외부 자극으로부터 신호를 받아들이는 역할을 하며, 세포체는 이 신호를 처리하고 통합합니다.
* 처리된 신호는 축삭을 통해 다음 뉴런이나 근육, 혹은 샘과 같은 다른 조직으로 전달됩니다.
* 축삭의 끝에는 시냅스(synapse)가 있어 화학적 신호 또는 전기적 신호를 통해 다른 세포와 연결됩니다.
* 뉴런은 이러한 작용을 통해 신경계가 복잡한 정보를 효율적으로 처리하고 전달할 수 있도록 돕습니다.
2. 인공 신경망
* 인공 신경망(Artificial Neural Network, ANN)은 생물학적 신경망의 구조와 기능을 모방한 계산 모델로, 여러 개의 인공 뉴런을 계층적으로 연결하여 구성됩니다.
* 기본적으로 입력층(input layer), 은닉층(hidden layer), 출력층(output layer)으로 이루어지며, 각 층의 뉴런들은 다음 층의 뉴런과 연결되어 데이터를 전달하고 처리합니다.
* 입력 데이터는 가중치와 활성화 함수 등의 연산을 거쳐 점차 복잡한 특징을 추출하며, 최종적으로 출력층에서 예측값이나 결과를 생성합니다.
* 신경망은 데이터에 기반한 학습을 통해 가중치를 조정하면서 문제를 해결하도록 최적화됩니다.
* 이러한 특성 덕분에 이미지 분류, 음성 인식, 자연어 처리 등 다양한 분야에서 뛰어난 성능을 발휘하며, 딥러닝의 주요 구성 요소로 활용됩니다.
* ANN은 다층 구조와 비선형 활성화 함수를 통해 복잡한 데이터 간의 관계를 학습할 수 있는 강력한 도구입니다.
3. 인공 신경망의 역사
1940년대 ~ 1980년대
* 인공 신경망(Artificial Neural Network, ANN)의 역사는 1940년대에 시작된 초기 개념부터 현대의 딥러닝에 이르기까지 긴 발전 과정을 거쳤습니다.
* 1943년, 워런 맥컬록(Warren McCulloch)과 월터 피츠(Walter Pitts)는 생물학적 뉴런을 수학적으로 모델링한 맥컬록-피츠 뉴런을 제안하며 ANN의 기초를 마련했습니다.
* 1958년, 프랭크 로젠블렛(Frank Rosenblatt)은 단층 퍼셉트론(perceptron)을 개발하여 ANN이 학습과 분류 문제를 해결할 수 있음을 보여주었습니다.
* 그러나 1969년, 마빈 민스키(Marvin Minsky)와 시모어 페이퍼트(Seymour Papert)는 퍼셉트론의 한계를 지적하며, 비선형 문제를 해결하지 못한다는 사실을 제시하였고, 이는 ANN 연구의 침체기로 이어졌습니다.
### 퍼셉트론
* 퍼셉트론(Perceptron)은 1958년 프랭크 로젠블렛(Frank Rosenblatt)이 제안한 인공 뉴런 모델로, 가장 간단한 형태의 인공 신경망입니다.
* 퍼셉트론은 입력 값과 해당 가중치(weight)의 곱을 모두 더한 값에 편향(bias)을 더하고, 이를 활성화 함수(보통 계단 함수)로 변환하여 이진 출력(0 또는 1)을 생성합니다.
* 학습 과정에서는 출력 값이 실제 값과 다를 경우, 가중치를 조정하는 방식으로 학습이 이루어집니다.
* 퍼셉트론은 단층 구조로 선형적으로 분리 가능한 문제를 해결할 수 있지만, XOR 문제와 같은 비선형적으로 분리되는 문제를 해결하지 못하는 한계가 있습니다.

예시 1)
# 논리 회귀(단층 퍼셉트론)로 AND 문제 해결하기
import torch # PyTorch 라이브러리
import torch.nn as nn # PyTorch의 신경망 모듈
import torch.optim as optim # PyTorch의 최적화 알고리즘 모듈
# 입력 데이터(X)와 정답 데이터(y) 정의
X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]])
# - X: 2차원 입력 데이터로, AND 문제의 입력값을 정의.
# - [0, 0], [0, 1], [1, 0], [1, 1]은 AND 연산의 입력 조합.
y = torch.FloatTensor([[0], [0], [0], [1]])
# - y: 입력값(X)에 대한 정답(출력) 데이터를 정의.
# - AND 연산의 결과:
# - 0 AND 0 = 0
# - 0 AND 1 = 0
# - 1 AND 0 = 0
# - 1 AND 1 = 1
# 모델 정의
model = nn.Sequential(
nn.Linear(2, 1), # 입력 2차원, 출력 1차원 (단층 퍼셉트론 구조)
nn.Sigmoid() # 출력값을 0~1 사이의 확률로 변환하는 활성화 함수
)
# - nn.Linear(2, 1):
# - 입력 데이터(X)의 차원(2)을 출력 차원(1)으로 선형 변환.
# - 선형 변환 공식: y = xWᵀ + b
# - nn.Sigmoid():
# - 출력값을 0~1 사이의 확률로 변환하여 논리 회귀 문제에 적합.
# 최적화 알고리즘 설정
optimizer = optim.SGD(model.parameters(), lr=1)
# - optim.SGD:
# - 확률적 경사 하강법(Stochastic Gradient Descent) 최적화 알고리즘.
# - model.parameters():
# - 모델에서 학습 가능한 매개변수(가중치와 편향)를 가져옴.
# - lr=1:
# - 학습률(learning rate)로, 매개변수를 업데이트할 때 사용하는 스텝 크기.
예시 2)
# 학습 루프 설정
epochs = 1000 # 총 학습 반복 횟수 설정
for epoch in range(epochs + 1): # 0부터 epochs까지 학습 반복
y_pred = model(X) # 모델에 입력 데이터를 전달하여 예측값 계산
# - y_pred: 모델이 계산한 출력값 (0~1 사이의 값, 확률 형태).
loss = nn.BCELoss()(y_pred, y)
# - nn.BCELoss():
# - 이진 크로스 엔트로피(Binary Cross Entropy) 손실 함수.
# - 예측값(y_pred)과 실제값(y)의 차이를 계산하여 손실값 반환.
optimizer.zero_grad() # 이전 그래디언트 초기화
loss.backward() # 손실값을 기반으로 그래디언트 계산 (역전파)
optimizer.step() # 계산된 그래디언트를 사용하여 모델의 매개변수 업데이트
if epoch % 100 == 0: # 100 에포크마다 결과 출력
y_bool = (y_pred >= 0.5).float()
# - (y_pred >= 0.5): 예측 확률(y_pred)이 0.5 이상인 경우 `1`, 미만인 경우 `0`.
# - .float(): 부울 값을 실수로 변환.
accuracy = (y == y_bool).float().sum() / len(y) * 100
# - (y == y_bool): 실제값(y)과 예측값(y_bool)을 비교하여 정확히 예측한 샘플만 `True`.
# - .float(): `True`와 `False`를 각각 1.0과 0.0으로 변환.
# - .sum(): 정확히 예측한 샘플의 개수를 계산.
# - / len(y): 정확히 예측한 비율 계산.
# - * 100: 정확도를 백분율로 변환.
print(f'Epoch {epoch:4d}/{epochs} Loss: {loss:.6f} Accuracy: {accuracy:.2f}%')
# - 현재 에포크 번호, 손실값, 정확도 출력.
# - f-string을 사용하여 손실값과 정확도를 포매팅.
---->
Epoch 0/1000 Loss: 0.610043 Accuracy: 75.00%
Epoch 100/1000 Loss: 0.140965 Accuracy: 100.00%
Epoch 200/1000 Loss: 0.080709 Accuracy: 100.00%
Epoch 300/1000 Loss: 0.056060 Accuracy: 100.00%
Epoch 400/1000 Loss: 0.042764 Accuracy: 100.00%
Epoch 500/1000 Loss: 0.034491 Accuracy: 100.00%
Epoch 600/1000 Loss: 0.028863 Accuracy: 100.00%
Epoch 700/1000 Loss: 0.024794 Accuracy: 100.00%
Epoch 800/1000 Loss: 0.021719 Accuracy: 100.00%
Epoch 900/1000 Loss: 0.019316 Accuracy: 100.00%
Epoch 1000/1000 Loss: 0.017386 Accuracy: 100.00%
예시 3)
# 논리 회귀(단층 퍼셉트론)로 OR 문제 해결하기
# OR 연산의 입력 데이터(X)와 정답 데이터(y) 정의
X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]])
# - X: OR 연산의 입력값을 정의.
# - [0, 0], [0, 1], [1, 0], [1, 1]은 OR 연산의 가능한 입력 조합.
y = torch.FloatTensor([[0], [1], [1], [1]])
# - y: 입력값(X)에 대한 정답(출력) 데이터를 정의.
# - OR 연산의 결과:
# - 0 OR 0 = 0
# - 0 OR 1 = 1
# - 1 OR 0 = 1
# - 1 OR 1 = 1
# 모델 정의
model = nn.Sequential(
nn.Linear(2, 1), # 입력 2차원, 출력 1차원 (단층 퍼셉트론 구조)
nn.Sigmoid() # 출력값을 0~1 사이의 확률로 변환하는 활성화 함수
)
# - nn.Linear(2, 1):
# - 입력 데이터(X)의 차원(2)을 출력 차원(1)으로 선형 변환.
# - 선형 변환 공식: y = xWᵀ + b
# - nn.Sigmoid():
# - 출력값을 0~1 사이로 변환하여 논리 회귀 문제에 적합.
# 최적화 알고리즘 설정
optimizer = optim.SGD(model.parameters(), lr=1)
# - optim.SGD:
# - 확률적 경사 하강법(Stochastic Gradient Descent) 최적화 알고리즘.
# - model.parameters():
# - 모델에서 학습 가능한 매개변수(가중치와 편향)를 가져옴.
# - lr=1:
# - 학습률(learning rate)로, 매개변수를 업데이트할 때 사용하는 스텝 크기.
# 학습 반복 횟수 설정
epochs = 1000
# 학습 루프
for epoch in range(epochs + 1): # 0부터 epochs까지 학습 반복
y_pred = model(X) # 모델에 입력 데이터를 전달하여 예측값 계산
# - y_pred: 모델이 계산한 출력값 (0~1 사이의 값, 확률 형태).
loss = nn.BCELoss()(y_pred, y)
# - nn.BCELoss():
# - 이진 크로스 엔트로피(Binary Cross Entropy) 손실 함수.
# - 예측값(y_pred)과 실제값(y)의 차이를 계산하여 손실값 반환.
optimizer.zero_grad() # 이전 그래디언트 초기화
loss.backward() # 손실값을 기반으로 그래디언트 계산 (역전파)
optimizer.step() # 계산된 그래디언트를 사용하여 모델의 매개변수 업데이트
if epoch % 100 == 0: # 100 에포크마다 결과 출력
y_bool = (y_pred >= 0.5).float()
# - (y_pred >= 0.5): 예측 확률(y_pred)이 0.5 이상인 경우 `1`, 미만인 경우 `0`.
# - .float(): 부울 값을 실수로 변환.
accuracy = (y == y_bool).float().sum() / len(y) * 100
# - (y == y_bool): 실제값(y)과 예측값(y_bool)을 비교하여 정확히 예측한 샘플만 `True`.
# - .float(): `True`와 `False`를 각각 1.0과 0.0으로 변환.
# - .sum(): 정확히 예측한 샘플의 개수를 계산.
# - / len(y): 정확히 예측한 비율 계산.
# - * 100: 정확도를 백분율로 변환.
print(f'Epoch {epoch:4d}/{epochs} Loss: {loss:.6f} Accuracy: {accuracy:.2f}%')
# - 현재 에포크 번호, 손실값, 정확도 출력.
# - f-string을 사용하여 손실값과 정확도를 포매팅.
---->
Epoch 0/1000 Loss: 0.604133 Accuracy: 75.00%
Epoch 100/1000 Loss: 0.088550 Accuracy: 100.00%
Epoch 200/1000 Loss: 0.046670 Accuracy: 100.00%
Epoch 300/1000 Loss: 0.031329 Accuracy: 100.00%
Epoch 400/1000 Loss: 0.023485 Accuracy: 100.00%
Epoch 500/1000 Loss: 0.018748 Accuracy: 100.00%
Epoch 600/1000 Loss: 0.015586 Accuracy: 100.00%
Epoch 700/1000 Loss: 0.013329 Accuracy: 100.00%
Epoch 800/1000 Loss: 0.011638 Accuracy: 100.00%
Epoch 900/1000 Loss: 0.010326 Accuracy: 100.00%
Epoch 1000/1000 Loss: 0.009277 Accuracy: 100.00%
예시 4)
# 논리 회귀(단층 퍼셉트론)로 XOR 문제 해결하기
# XOR 연산의 입력 데이터(X)와 정답 데이터(y) 정의
X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]])
# - X: XOR 연산의 입력값을 정의.
# - [0, 0], [0, 1], [1, 0], [1, 1]은 XOR 연산의 가능한 입력 조합.
y = torch.FloatTensor([[0], [1], [1], [0]])
# - y: 입력값(X)에 대한 정답(출력) 데이터를 정의.
# - XOR 연산의 결과:
# - 0 XOR 0 = 0
# - 0 XOR 1 = 1
# - 1 XOR 0 = 1
# - 1 XOR 1 = 0
# 모델 정의
model = nn.Sequential(
nn.Linear(2, 1), # 입력 2차원, 출력 1차원 (단층 퍼셉트론 구조)
nn.Sigmoid() # 출력값을 0~1 사이의 확률로 변환하는 활성화 함수
)
# - nn.Linear(2, 1):
# - 입력 데이터(X)의 차원(2)을 출력 차원(1)으로 선형 변환.
# - 선형 변환 공식: y = xWᵀ + b
# - nn.Sigmoid():
# - 출력값을 0~1 사이로 변환하여 논리 회귀 문제에 적합.
# 최적화 알고리즘 설정
optimizer = optim.SGD(model.parameters(), lr=1)
# - optim.SGD:
# - 확률적 경사 하강법(Stochastic Gradient Descent) 최적화 알고리즘.
# - model.parameters():
# - 모델에서 학습 가능한 매개변수(가중치와 편향)를 가져옴.
# - lr=1:
# - 학습률(learning rate)로, 매개변수를 업데이트할 때 사용하는 스텝 크기.
# 학습 반복 횟수 설정
epochs = 1000
# 학습 루프
for epoch in range(epochs + 1): # 0부터 epochs까지 학습 반복
y_pred = model(X) # 모델에 입력 데이터를 전달하여 예측값 계산
# - y_pred: 모델이 계산한 출력값 (0~1 사이의 값, 확률 형태).
loss = nn.BCELoss()(y_pred, y)
# - nn.BCELoss():
# - 이진 크로스 엔트로피(Binary Cross Entropy) 손실 함수.
# - 예측값(y_pred)과 실제값(y)의 차이를 계산하여 손실값 반환.
optimizer.zero_grad() # 이전 그래디언트 초기화
loss.backward() # 손실값을 기반으로 그래디언트 계산 (역전파)
optimizer.step() # 계산된 그래디언트를 사용하여 모델의 매개변수 업데이트
if epoch % 100 == 0: # 100 에포크마다 결과 출력
y_bool = (y_pred >= 0.5).float()
# - (y_pred >= 0.5): 예측 확률(y_pred)이 0.5 이상인 경우 `1`, 미만인 경우 `0`.
# - .float(): 부울 값을 실수로 변환.
accuracy = (y == y_bool).float().sum() / len(y) * 100
# - (y == y_bool): 실제값(y)과 예측값(y_bool)을 비교하여 정확히 예측한 샘플만 `True`.
# - .float(): `True`와 `False`를 각각 1.0과 0.0으로 변환.
# - .sum(): 정확히 예측한 샘플의 개수를 계산.
# - / len(y): 정확히 예측한 비율 계산.
# - * 100: 정확도를 백분율로 변환.
print(f'Epoch {epoch:4d}/{epochs} Loss: {loss:.6f} Accuracy: {accuracy:.2f}%')
# - 현재 에포크 번호, 손실값, 정확도 출력.
# - f-string을 사용하여 손실값과 정확도를 포매팅.
--->
Epoch 0/1000 Loss: 0.707292 Accuracy: 25.00%
Epoch 100/1000 Loss: 0.693147 Accuracy: 50.00%
Epoch 200/1000 Loss: 0.693147 Accuracy: 75.00%
Epoch 300/1000 Loss: 0.693147 Accuracy: 50.00%
Epoch 400/1000 Loss: 0.693147 Accuracy: 50.00%
Epoch 500/1000 Loss: 0.693147 Accuracy: 50.00%
Epoch 600/1000 Loss: 0.693147 Accuracy: 50.00%
Epoch 700/1000 Loss: 0.693147 Accuracy: 50.00%
Epoch 800/1000 Loss: 0.693147 Accuracy: 50.00%
Epoch 900/1000 Loss: 0.693147 Accuracy: 50.00%
Epoch 1000/1000 Loss: 0.693147 Accuracy: 50.00%
### 1980년대 ~ 2000년대
* 1980년대에 이르러 역전파(backpropagation) 알고리즘이 재발견되면서 ANN이 다시 주목받기 시작했습니다.
* 특히 제프리 힌턴(Geoffrey Hinton) 등 연구자들의 공헌으로 다층 퍼셉트론(Multi-Layer Perceptron, MLP)이 비선형 문제를 해결할 수 있음을 보였고, ANN 연구가 활발해졌습니다.
* 1990년대에는 합성곱 신경망(CNN)과 순환 신경망(RNN) 등 특화된 구조가 개발되며 ANN이 더 복잡한 문제를 다룰 수 있게 되었습니다.

예시 1)
# 다층 퍼셉트론(Multi-Layer Perceptron, MLP) 모델 정의
model = nn.Sequential(
nn.Linear(2, 4), # 첫 번째 선형 계층: 입력(2차원) → 은닉층(4차원)
nn.Sigmoid(), # 활성화 함수: Sigmoid (은닉층의 비선형성 추가)
nn.Linear(4, 1), # 두 번째 선형 계층: 은닉층(4차원) → 출력(1차원)
nn.Sigmoid() # 활성화 함수: Sigmoid (출력을 0~1 사이 확률로 변환)
)
# - nn.Sequential:
# - 계층을 순차적으로 쌓아 신경망을 정의.
# - 각 계층은 순서대로 연결되어 데이터를 처리.
# - nn.Linear(in_features, out_features):
# - 선형 변환 계층(fully connected layer).
# - 입력 크기(`in_features`)에서 출력 크기(`out_features`)로 변환.
# - nn.Sigmoid():
# - 활성화 함수로, 각 출력값을 0~1 사이의 값으로 변환.
# - 비선형성을 추가하여 XOR와 같은 비선형 문제를 해결 가능.
# 모델 구조 출력
print(model)
# - 모델의 계층 구조를 출력하여 확인.
--->
Sequential(
(0): Linear(in_features=2, out_features=4, bias=True)
(1): Sigmoid()
(2): Linear(in_features=4, out_features=1, bias=True)
(3): Sigmoid()
)--->

예시 2)
# 논리 회귀(다층 퍼셉트론)로 XOR 문제 해결하기
# XOR 연산의 입력 데이터(X)와 정답 데이터(y) 정의
X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]])
# - X: XOR 연산의 입력값을 정의.
# - [0, 0], [0, 1], [1, 0], [1, 1]은 XOR 연산의 가능한 입력 조합.
y = torch.FloatTensor([[0], [1], [1], [0]])
# - y: 입력값(X)에 대한 정답(출력) 데이터를 정의.
# - XOR 연산의 결과:
# - 0 XOR 0 = 0
# - 0 XOR 1 = 1
# - 1 XOR 0 = 1
# - 1 XOR 1 = 0
# 최적화 알고리즘 설정
optimizer = optim.SGD(model.parameters(), lr=1)
# - optim.SGD:
# - 확률적 경사 하강법(Stochastic Gradient Descent) 최적화 알고리즘.
# - model.parameters():
# - 모델에서 학습 가능한 매개변수(가중치와 편향)를 가져옴.
# - lr=1:
# - 학습률(learning rate)로, 매개변수를 업데이트할 때 사용하는 스텝 크기.
# 학습 반복 횟수 설정
epochs = 1000
# 학습 루프
for epoch in range(epochs + 1): # 0부터 epochs까지 학습 반복
y_pred = model(X) # 모델에 입력 데이터를 전달하여 예측값 계산
# - y_pred: 모델이 계산한 출력값 (0~1 사이의 값, 확률 형태).
loss = nn.BCELoss()(y_pred, y)
# - nn.BCELoss():
# - 이진 크로스 엔트로피(Binary Cross Entropy) 손실 함수.
# - 예측값(y_pred)과 실제값(y)의 차이를 계산하여 손실값 반환.
optimizer.zero_grad() # 이전 그래디언트 초기화
loss.backward() # 손실값을 기반으로 그래디언트 계산 (역전파)
optimizer.step() # 계산된 그래디언트를 사용하여 모델의 매개변수 업데이트
if epoch % 100 == 0: # 100 에포크마다 결과 출력
y_bool = (y_pred >= 0.5).float()
# - (y_pred >= 0.5): 예측 확률(y_pred)이 0.5 이상인 경우 `1`, 미만인 경우 `0`.
# - .float(): 부울 값을 실수로 변환.
accuracy = (y == y_bool).float().sum() / len(y) * 100
# - (y == y_bool): 실제값(y)과 예측값(y_bool)을 비교하여 정확히 예측한 샘플만 `True`.
# - .float(): `True`와 `False`를 각각 1.0과 0.0으로 변환.
# - .sum(): 정확히 예측한 샘플의 개수를 계산.
# - / len(y): 정확히 예측한 비율 계산.
# - * 100: 정확도를 백분율로 변환.
print(f'Epoch {epoch:4d}/{epochs} Loss: {loss:.6f} Accuracy: {accuracy:.2f}%')
# - 현재 에포크 번호, 손실값, 정확도 출력.
# - f-string을 사용하여 손실값과 정확도를 포매팅.
--->
Epoch 0/1000 Loss: 0.696326 Accuracy: 50.00%
Epoch 100/1000 Loss: 0.693282 Accuracy: 50.00%
Epoch 200/1000 Loss: 0.693132 Accuracy: 50.00%
Epoch 300/1000 Loss: 0.693015 Accuracy: 50.00%
Epoch 400/1000 Loss: 0.692822 Accuracy: 50.00%
Epoch 500/1000 Loss: 0.692270 Accuracy: 50.00%
Epoch 600/1000 Loss: 0.689365 Accuracy: 50.00%
Epoch 700/1000 Loss: 0.657556 Accuracy: 75.00%
Epoch 800/1000 Loss: 0.475295 Accuracy: 75.00%
Epoch 900/1000 Loss: 0.142640 Accuracy: 100.00%
Epoch 1000/1000 Loss: 0.055724 Accuracy: 100.00%
4. 비선형 활성화 함수
* 비선형 활성화 함수는 신경망에서 선형 변환만으로는 표현할 수 없는 복잡한 비선형 패턴을 학습할 수 있도록 도와주는 함수입니다.
* 입력 값을 비선형적으로 변환하여 신경망의 계층마다 다른 특징을 학습하게 하며, 이를 통해 선형 함수들의 조합으로는 표현할 수 없는 복잡한 함수와 데이터 분포를 모델링할 수 있습니다.
* 주요 예로 ReLU, Sigmoid, Tanh 등이 있으며, 이 함수들은 출력 값을 제한하거나 왜곡하여 학습을 안정화하고, 신경망이 더 강력한 표현력을 가지도록 만듭니다.
### 1-1. 시크모이드
# 필요한 라이브러리 임포트
import numpy as np # 수치 계산을 위한 라이브러리
import matplotlib.pyplot as plt # 데이터 시각화를 위한 라이브러리
# Sigmoid 함수 정의
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# - np.exp(-x): x 값에 대한 지수 함수(e^(-x))를 계산.
# - 1 / (1 + np.exp(-x)): Sigmoid 함수 공식.
# - 입력값(x)을 0~1 사이로 변환.
# - x가 음수일수록 출력값은 0에 가까워지고,
# x가 양수일수록 출력값은 1에 가까워짐.
# x 값의 범위 설정
x = np.arange(-5.0, 5.0, 0.1)
# - np.arange(start, stop, step):
# - -5.0부터 5.0까지 0.1 간격으로 값을 생성.
# - 결과는 [-5.0, -4.9, ..., 4.9]와 같은 배열.
# Sigmoid 함수 적용
y = sigmoid(x)
# - x 배열의 각 원소에 대해 Sigmoid 함수 값을 계산하여 y 배열 생성.
# Sigmoid 함수 시각화
plt.plot(x, y) # x와 y 값을 사용해 그래프를 그림.
plt.plot([0, 0], [1.0, 0.0], ':')
# - [0, 0]: x축에서 0을 기준으로 수직선을 그림.
# - [1.0, 0.0]: y축의 시작(1.0)과 끝(0.0)을 연결.
# - ':'은 점선 스타일을 의미.
plt.title('Sigmoid Function') # 그래프 제목 설정.
plt.show() # 그래프 출력.---->

### 4-2. 하이퍼볼릭탄젠트
* 하이퍼볼릭 탄젠트(흔히 Tanh 함수라고 불림)는 비선형 활성화 함수 중 하나로, 입력 값을 -1에서 1 사이의 값으로 변환하는 함수입니다.
* 입력 값이 큰 양수일수록 1에 가까워지고, 큰 음수일수록 -1에 가까워집니다.
* 이 함수는 출력 범위가 대칭적이어서 Sigmoid 함수와 달리 출력이 0을 기준으로 분포되므로, 데이터가 양수와 음수로 분리되는 문제에서 더 적합합니다.
* 그러나 입력 값이 매우 크거나 작을 경우 기울기가 거의 0에 가까워지는 "기울기 소실" 문제가 발생할 수 있습니다.
* Tanh는 주로 출력 값의 분포를 중심에 맞추고 싶을 때 사용됩니다.
예시 1)
# 필요한 라이브러리 임포트
import numpy as np # 수치 계산을 위한 라이브러리
import matplotlib.pyplot as plt # 데이터 시각화를 위한 라이브러리
# x 값의 범위 설정
x = np.arange(-5.0, 5.0, 0.1)
# - np.arange(start, stop, step):
# - -5.0부터 5.0까지 0.1 간격으로 값을 생성.
# - 결과는 [-5.0, -4.9, ..., 4.9]와 같은 배열.
# Tanh 함수 적용
y = np.tanh(x)
# - np.tanh(x):
# - 입력값(x)에 대해 쌍곡탄젠트(Tanh) 함수를 적용.
# - Tanh 함수 공식:
# \[
# \text{Tanh}(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}
# \]
# - 결과는 [-1, 1] 범위의 값을 반환.
# - x가 음수일수록 출력값은 -1에 가까워지고,
# x가 양수일수록 출력값은 1에 가까워짐.
# Tanh 함수 시각화
plt.plot(x, y) # x와 y 값을 사용해 Tanh 함수 그래프를 그림.
plt.plot([0, 0], [1.0, 0.0], ':')
# - [0, 0]: x축에서 0을 기준으로 수직선을 그림.
# - [1.0, 0.0]: y축의 시작(1.0)과 끝(0.0)을 연결.
# - ':'은 점선 스타일을 의미.
plt.axhline(y=0, color='orange', linestyle='--')
# - axhline(y=0): y=0에 가로선(수평선)을 그림.
# - color='orange': 수평선의 색상을 주황색으로 설정.
# - linestyle='--': 수평선을 점선 스타일로 설정.
plt.title('Tanh Function') # 그래프 제목 설정.
plt.show() # 그래프 출력.---->

### 4-3. 렐루(Rectified Linear Unit)
* ReLU(Rectified Linear Unit)는 신경망에서 가장 널리 사용되는 비선형 활성화 함수 중 하나로, 입력 값이 0보다 크면 그대로 출력하고, 0 이하이면 0을 출력하는 함수입니다.
* 출력 값이 양수인 경우 기울기가 1로 일정하게 유지되므로 기울기 소실 문제를 완화할 수 있습니다.
* 이로 인해 학습이 빠르고 효율적이며, 깊은 신경망에서 성능이 뛰어난 것으로 알려져 있습니다.
* 그러나 ReLU는 입력 값이 0 이하일 때 기울기가 0이 되어 학습되지 않는 "죽은 ReLU" 문제가 발생할 수 있으며, 이를 보완하기 위해 Leaky ReLU와 같은 변형 함수들이 개발되었습니다.
예시 1)
# ReLU (Rectified Linear Unit) 함수 시각화
plt.plot(x, y)
# - x: 입력 데이터.
# - y: ReLU 함수가 적용된 출력값(양수는 그대로, 음수는 0으로 변환).
# - x와 y를 사용하여 ReLU 함수의 그래프를 그림.
plt.plot([0, 0], [5.0, 0.0], ':')
# - [0, 0]: x축에서 0을 기준으로 수직선을 그림.
# - [5.0, 0.0]: y축의 시작(5.0)과 끝(0.0)을 연결.
# - ':'은 점선 스타일로 설정하여 보조선을 강조.
plt.title('ReLU Function')
# - 그래프 제목을 "ReLU Function"으로 설정.
plt.show()
# - 그래프를 출력하여 화면에 표시.--->


##4-4. 소프트맥스
예시 1)
# Softmax 함수 구현 및 시각화
# x 값의 범위 설정
x = np.arange(-5.0, 5.0, 0.1)
# - np.arange(start, stop, step):
# - -5.0부터 5.0까지 0.1 간격으로 값을 생성.
# - 결과는 [-5.0, -4.9, ..., 4.9]와 같은 배열.
# Softmax 함수 계산
y = np.exp(x) / np.sum(np.exp(x))
# - np.exp(x): x 배열의 각 요소에 대해 지수 함수(e^x)를 계산.
# - np.sum(np.exp(x)): x 배열의 모든 요소에 대해 e^x 값을 계산한 후 합산.
# - Softmax 공식:
# \[
# S(x_i) = \frac{e^{x_i}}{\sum_{j} e^{x_j}}
# \]
# - 입력값을 확률 분포로 변환하여 각 값이 0~1 사이에 속하며, 전체 합은 1이 됨.
# Softmax 함수 시각화
plt.plot(x, y) # x와 y 값을 사용해 Softmax 함수 그래프를 그림.
plt.title('Softmax Function') # 그래프 제목을 "Softmax Function"으로 설정.
plt.show() # 그래프를 출력.--->

'LLM(Large Language Model)의 기초 > 딥러닝' 카테고리의 다른 글
| 4. 손글씨 도형 분류하기 (0) | 2025.01.16 |
|---|---|
| 3. CNN(Convolutional Neural Network, 합성곱 신경망) (2) | 2025.01.15 |
| 2. Multi-class Weather Dataset (2) | 2025.01.14 |