2025. 1. 15. 11:47ㆍLLM(Large Language Model)의 기초/딥러닝
1.CNN
* CNN(Convolutional Neural Network, 합성곱 신경망)은 주로 이미지나 비정형 데이터의 패턴을 학습하고 분석하는 데 사용되는 딥러닝 모델입니다.
* CNN은 이미지의 공간적 구조를 효율적으로 처리하기 위해 합성곱 계층(convolutional layer)을 사용하며, 이 계층은 필터(커널)를 통해 입력 데이터에서 중요한 특징(에지, 모양 등)을 추출합니다.
* 이어서 풀링 계층(pooling layer)을 통해 차원을 축소하고 계산 효율을 높이며, 마지막으로 완전 연결 계층(fully connected layer)을 사용해 특정 클래스나 값을 예측합니다.
* CNN은 이미지 분류, 객체 탐지, 영상 처리 등 다양한 분야에서 높은 성능을 발휘하며, 이미지의 공간적 관계를 보존하면서 학습할 수 있다는 점에서 강점을 가집니다.
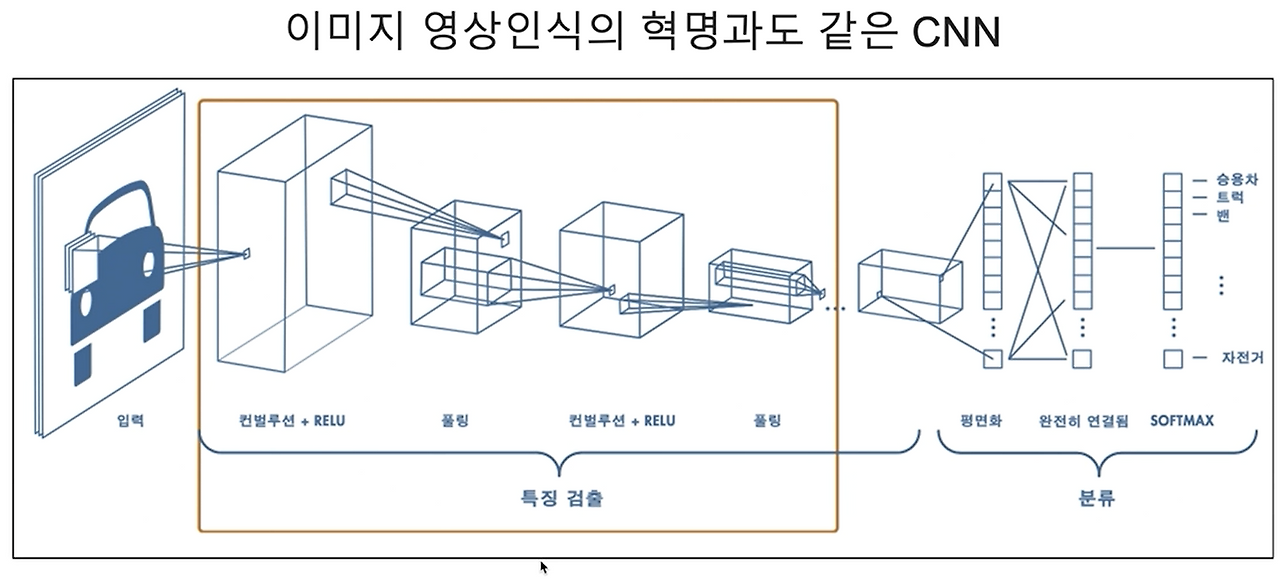
### 영상처리에서 CNN을 사용하는 이유
* 영상처리에서 CNN을 사용하는 이유는 이미지를 분석하는 데 더 적합한 구조를 가지고 있기 때문입니다.
* CNN은 작은 필터를 사용해 이미지에서 중요한 특징(예: 선, 모양 등)을 효율적으로 추출하며, 이를 반복적으로 사용해 학습해야 할 양을 줄입니다.
* 또한, 이미지가 조금 이동하거나 변형되어도 특징을 잘 인식할 수 있고, 간단한 요소에서 복잡한 패턴까지 단계적으로 분석할 수 있어 DNN보다 더 적합합니다.
* DNN은 모든 픽셀을 개별적으로 학습하려 하기 때문에 계산이 복잡하고 이미지의 공간적 구조를 잘 반영하지 못합니다.
2.입력 이미지
* 컴퓨터가 이미지를 인식하는 과정은 이미지를 숫자로 표현하는 것에서 시작됩니다.
* 이미지는 픽셀 값(흑백 이미지는 밝기를 0~255 사이 숫자로, 컬러 이미지는 RGB 채널 값으로)을 가진 행렬로 변환되며, 이 숫자 데이터를 기반으로 컴퓨터가 계산을 수행합니다.

참고 : 64 * 64개의 4096개의 점으로 그림이 이루어져있다
즉, 12,288개의 그림으로 이루어져있다
3. 합성곱 계층
* 합성곱 계층(Convolution Layer)은 CNN(Convolutional Neural Network)의 핵심 구성 요소로, 이미지에서 중요한 특징을 추출하는 역할을 합니다.
* 이 계층은 작은 크기의 필터(커널)를 사용해 입력 데이터(이미지)의 일부분과 합성곱 연산을 수행하며, 필터는 특정 패턴(예: 가장자리, 텍스처 등)을 감지하도록 학습됩니다.
* 필터는 이미지를 스캔하며 각 위치에서 특징 맵(feature map)을 생성하는데, 이는 이미지의 중요한 정보를 강조한 새로운 데이터 표현입니다.
* Convolution Layer는 이미지의 공간적 구조를 보존하면서 효율적으로 특징을 추출하고, 이를 다음 계층으로 전달해 점점 더 복잡한 패턴을 학습할 수 있게 합니다.
3-1.합성곱 연산
* 합성곱 연산(Convolution Operation)은 합성곱 계층에서 입력 데이터(예: 이미지)와 필터(커널)를 사용해 특징을 추출하는 기본 과정입니다.
* 이 연산은 필터를 이미지 위에서 일정한 크기만큼 이동하며, 필터와 해당 영역의 픽셀 값을 element-wise 곱한 뒤 합산하여 하나의 값을 생성합니다.
* 이 과정으로 생성된 값들이 모여 새로운 특징 맵(feature map)을 만듭니다.
* 필터는 학습 과정에서 업데이트되며, 특정 패턴(예: 가장자리, 선, 질감 등)을 감지할 수 있도록 조정됩니다.
* 합성곱 연산은 이미지의 공간적 관계를 보존하면서도 중요한 정보를 강조하고, 불필요한 정보를 줄이는 데 매우 효과적입니다.

3-2.스트라이드
* 스트라이드(Stride)는 합성곱 연산에서 필터(커널)가 입력 데이터(이미지) 위를 이동하는 간격을 의미합니다.
* 기본적으로 스트라이드 값이 1이면 필터가 한 칸씩 움직이며 모든 위치에서 연산을 수행합니다.
* 스트라이드 값이 2 이상이면 필터가 더 큰 간격으로 이동하므로, 생성되는 출력 크기가 작아지고 연산량도 줄어듭니다.
* 스트라이드를 조절하면 특징 맵의 크기를 조정할 수 있어, 모델의 계산 효율성을 높이거나 더 큰 영역의 정보를 한 번에 처리할 수 있습니다.
* 다만, 스트라이드가 너무 크면 중요한 세부 정보가 손실될 수 있으므로 적절한 값을 선택하는 것이 중요합니다.

3-3. 패딩
* 패딩(Padding)은 합성곱 연산에서 입력 데이터(이미지)의 가장자리에 값을 추가하여 출력 크기를 조정하거나 경계 부분의 정보 손실을 방지하는 기법입니다.
* 일반적으로 가장자리에 0을 추가하는 제로 패딩(Zero Padding)이 많이 사용됩니다. 패딩은 두 가지 주요 목적이 있습니다:
* 첫째, 입력 데이터 크기를 유지하여 출력 크기를 줄이지 않고 처리할 수 있게 하며(예: "same" 패딩),
* 둘째, 경계 부분의 정보를 더 많이 학습할 수 있게 합니다.
* 패딩을 사용하지 않으면("valid" 패딩) 합성곱 연산이 진행될수록 데이터 크기가 줄어드는 문제가 발생할 수 있습니다. 이를 통해 모델이 공간 정보를 더 잘 학습할 수 있도록 돕습니다.

3-4. 풀링
* 풀링(Pooling)은 CNN에서 특징 맵의 크기를 줄이고, 중요한 정보를 요약하여 계산 효율성을 높이는 과정입니다.
* 주로 사용되는 방법은 최대 풀링(Max Pooling)과 평균 풀링(Average Pooling)으로, 최대 풀링은 작은 영역에서 가장 큰 값을 선택해 주요 특징을 강조하고, 평균 풀링은 영역의 평균값을 계산하여 전체적인 정보를 요약합니다.
* 풀링은 데이터 크기를 줄이면서도 중요한 특징을 유지하고, 모델이 공간적 위치 변화에 덜 민감해지도록 만들어 일반화 성능을 높입니다.
* 이를 통해 연산량을 줄이고 과적합(overfitting)을 방지하는 데 도움을 줍니다.

4. DNN과 CNN
4-1. DNN의 가중치와 편향
* DNN은 완전 연결 계층(fully connected layer)으로 구성되어 있어, 각 입력 노드가 모든 출력 노드와 연결됩니다.
* 이 때문에 입력 노드의 수와 출력 노드의 수에 비례하여 매우 많은 가중치(weight)가 필요합니다.
* 각 연결마다 고유한 가중치를 학습하므로, 같은 값이라도 위치가 다르면 별도의 가중치를 사용합니다.
* 모든 노드에 대해 별도로 편향(bias)이 존재하며, 가중치와 함께 학습됩니다.
4-2. CNN의 가중치와 편항
* CNN의 합성곱 계층은 작은 크기의 필터(커널)를 사용하여 입력 데이터의 특정 영역만을 처리합니다.
* 필터는 여러 위치에서 동일하게 적용되며, 이를 **가중치 공유(weight sharing)**라고 합니다.
* 즉, 필터에 사용되는 가중치는 입력 데이터의 모든 영역에서 반복적으로 사용되므로, 학습해야 할 가중치 수가 크게 줄어듭니다.
* 각 필터마다 하나의 편향(bias)이 있으며, 필터가 어디에 적용되든 동일하게 사용됩니다.
* 합성곱 신경망에도 편향(bias)을 추가할 수 있습니다.
* 만약, 편향을 사용한다면 커널을 적용한 뒤에 더해집니다. 편향은 하나의 값만 존재하며, 커널이 적용된 결과의 모든 원소에 더해집니다.


5. 다수의 채널 합성곱 연산
다수의 채널을 가진 경우(예: 컬러 이미지는 3개의 채널, RGB로 구성됨), 합성곱 연산은 각 채널별로 개별적으로 진행된 후 합산되어 최종적인 결과를 도출합니다.
* 필터의 각 채널과 입력 이미지의 대응 채널에 대해 합성곱 연산을 수행합니다. (예를 들어, 필터의 R 채널 부분과 이미지의 R 채널 부분에서 합성곱 연산을 수행합니다.
* 동일하게 G 채널과 B 채널에서도 각각 수행됩니다.)
* 각 채널에서 나온 합성곱 결과를 더해서 최종 값 하나를 만듭니다.
* 필터는 설정된 스트라이드에 따라 이미지 위를 이동하며 위 과정을 반복합니다.
* 최종적으로 각 위치에서 계산된 결과값들이 모여 하나의 출력 채널(feature map)을 형성합니다.

6. CNN을 구성하는 레이어
CNN은 주로 다음과 같은 레이어로 구성되며, 이미지를 단계적으로 처리해서 결과를 예측합니다. (CNN 체험하기)
CNN 체험 링크 : https://adamharley.com/nn_vis/
* 입력 레이어
* 이미지를 숫자 행렬(예: 32×32×3, RGB 채널)로 네트워크에 전달합니다.
* 합성곱 레이어(Convolution Layer)
* 작은 필터(예: 3×3)를 사용해 이미지의 중요한 특징(예: 선, 모양 등)을 찾아냅니다.
* 필터를 여러 개 사용해 여러 가지 특징을 추출합니다.
* 활성화 함수(ReLU)
* 음수 값을 0으로 바꿔 비선형성을 추가하고, 모델이 복잡한 패턴을 학습할 수 있도록 돕습니다.
* 풀링 레이어(Pooling Layer)
* 이미지 크기를 줄이고 중요한 정보만 요약합니다.
* 예: 2×2풀링은 4개의 값 중 가장 큰 값을 선택(Max Pooling).
* 완전 연결 계층(Fully Connected Layer)
* 이미지의 모든 특징을 하나의 벡터로 평평하게 펼쳐 최종 클래스를 예측합니다.
* 예: 10개의 클래스(고양이, 개 등)에 대해 확률을 계산합니다.
* 출력 레이어(Output Layer)
* 소프트맥스(Softmax) 같은 함수를 사용해 각 클래스에 대한 확률을 출력합니다.
7.간단한 CNN 모델 만들기
예시 1)
import torch
import torch.nn as nn
import torch.optim as optim
# inputs 텐서 생성: 배치 크기 1, 채널 1(그레이스케일 이미지), 너비 28, 높이 28
# - 배치 크기(batch size): 한번에 처리할 데이터 샘플의 개수. 여기서는 1개의 이미지.
# - 채널(channels): 이미지의 색상 채널. 1은 그레이스케일(흑백 이미지), 3은 RGB(컬러 이미지).
# - 너비(width): 이미지의 가로 픽셀 크기.
# - 높이(height): 이미지의 세로 픽셀 크기.
inputs = torch.Tensor(1, 1, 28, 28)
# 텐서의 shape 확인. 결과는 (1, 1, 28, 28)
# - 첫 번째 값: 배치 크기 (1)
# - 두 번째 값: 채널 수 (1)
# - 세 번째 값: 너비 (28)
# - 네 번째 값: 높이 (28)
print(inputs.shape)
--->
torch.Size([1, 1, 28, 28])
예시 2)
# 3 * 3 필터 32개의 필터를 사용해 32개의 특징 맵을 생성
# nn.Sequential: 여러 층을 순차적으로 연결하여 모델을 구성하는 클래스.
conv1 = nn.Sequential(
nn.Conv2d(
in_channels=1, # 입력 채널 수: 1 (그레이스케일 이미지)
out_channels=32, # 출력 채널 수: 32 (특징 맵 개수)
kernel_size=3, # 커널(필터)의 크기: 3x3
padding='same' # 패딩 설정: 'same'은 출력 크기를 입력 크기와 동일하게 유지
),
nn.ReLU() # ReLU 활성화 함수: 비선형성을 추가하여 모델의 표현력을 높임
)
# conv1을 입력 텐서(inputs)에 적용하여 출력 텐서(out) 생성
out = conv1(inputs)
# 출력 텐서의 shape 확인
# (1, 32, 28, 28):
# - 배치 크기: 1 (입력과 동일)
# - 출력 채널 수: 32 (필터 개수와 동일)
# - 너비: 28 (패딩 'same' 설정으로 입력과 동일)
# - 높이: 28 (패딩 'same' 설정으로 입력과 동일)
print(out.shape)
---->
torch.Size([1, 32, 28, 28])
예시 3)
# MaxPool2d: 최대 풀링 연산을 수행하여 특징 맵의 크기를 축소
# - kernel_size=2: 2x2 크기의 풀링 창을 사용
# - stride(기본값=2): 풀링 창을 이동하는 간격. 기본값으로 커널 크기와 동일(2).
# - 기본값을 사용할 경우, 출력 크기는 입력 크기의 절반으로 줄어듦.
# - stride=1로 설정하면 출력 크기가 입력 크기에서 1만큼 감소.
pool1 = nn.MaxPool2d(kernel_size=2)
# MaxPool2d를 입력 텐서(out)에 적용하여 출력 텐서(out) 생성
out = pool1(out)
# 출력 텐서의 shape 확인
# (1, 32, 14, 14):
# - 배치 크기: 1 (변화 없음)
# - 채널 수: 32 (변화 없음)
# - 너비와 높이: 14x14 (28x28에서 2x2 풀링으로 크기가 절반으로 줄어듦)
print(out.shape)
--->
torch.Size([1, 32, 14, 14])
예시 4)
# 두 번째 컨볼루션 계층 정의
conv2 = nn.Sequential(
nn.Conv2d(
in_channels=32, # 입력 채널 수: 32 (이전 계층의 출력 채널 수와 동일)
out_channels=64, # 출력 채널 수: 64 (64개의 필터 사용)
kernel_size=3, # 커널(필터)의 크기: 3x3
padding='same' # 패딩 설정: 'same'은 출력 크기를 입력 크기와 동일하게 유지
),
nn.ReLU() # ReLU 활성화 함수: 비선형성을 추가하여 표현력 향상
)
# conv2를 이전 계층의 출력 텐서(out)에 적용하여 새로운 출력 텐서(out) 생성
out = conv2(out)
# 출력 텐서의 shape 확인
# (1, 64, 14, 14):
# - 배치 크기: 1 (변화 없음)
# - 출력 채널 수: 64 (필터 개수와 동일)
# - 너비와 높이: 14x14 (입력 크기와 동일. 패딩 'same' 설정으로 크기 유지)
print(out.shape)
--->
torch.Size([1, 64, 14, 14])
예시 5)
# 두 번째 최대 풀링 계층 정의
# MaxPool2d: 최대 풀링 연산을 수행하여 특징 맵의 크기를 축소
# - kernel_size=2: 2x2 크기의 풀링 창 사용
# - stride(기본값=2): 풀링 창을 이동하는 간격. 기본값으로 커널 크기와 동일(2).
# - 기본값을 사용할 경우, 출력 크기는 입력 크기의 절반으로 줄어듦.
pool2 = nn.MaxPool2d(kernel_size=2)
# pool2를 이전 계층의 출력 텐서(out)에 적용하여 새로운 출력 텐서(out) 생성
out = pool2(out)
# 출력 텐서의 shape 확인
# (1, 64, 7, 7):
# - 배치 크기: 1 (변화 없음)
# - 출력 채널 수: 64 (변화 없음)
# - 너비와 높이: 7x7 (14x14에서 2x2 풀링으로 크기가 절반으로 줄어듦)
print(out.shape)
--->
torch.Size([1, 64, 7, 7])
예시 6)
# Flatten 계층 정의
# nn.Flatten: 다차원 텐서를 1차원 벡터로 변환
# - 특징 맵의 공간적 크기(가로, 세로)를 하나의 차원으로 펼쳐줌
flatten = nn.Flatten()
# flatten 계층을 이전 계층의 출력 텐서(out)에 적용하여 새로운 출력 텐서(out) 생성
out = flatten(out)
# 출력 텐서의 shape 확인
# (1, 64 * 7 * 7):
# - 배치 크기: 1 (변화 없음)
# - 특징 벡터 크기: 64 * 7 * 7 = 3136
# - 64는 채널 수(필터 개수)
# - 7x7은 각 채널의 너비와 높이를 펼친 결과
print(out.shape) # (1, 3136)
--->
torch.Size([1, 3136])
예제 7)
# 완전 연결 계층(fully connected layer) 정의
fc = nn.Sequential(
nn.Dropout(0.5), # Dropout: 신경망의 일부 노드를 랜덤하게 비활성화하여 과적합 방지
# - 0.5: 전체 노드 중 50%를 랜덤하게 비활성화
nn.Linear(3136, 10) # Linear: 입력과 출력을 연결하는 선형 변환
# - 입력 크기: 3136 (Flatten된 벡터 크기)
# - 출력 크기: 10 (분류할 클래스 수)
)
# fc 계층을 이전 계층의 출력 텐서(out)에 적용하여 새로운 출력 텐서(out) 생성
out = fc(out)
# 출력 텐서의 shape 확인
# (1, 10):
# - 배치 크기: 1 (변화 없음)
# - 출력 크기: 10 (클래스의 개수, 예: 10개의 분류 대상)
print(out.shape) # (1, 10)
--->
torch.Size([1, 10])'LLM(Large Language Model)의 기초 > 딥러닝' 카테고리의 다른 글
| 4. 손글씨 도형 분류하기 (0) | 2025.01.16 |
|---|---|
| 2. Multi-class Weather Dataset (2) | 2025.01.14 |
| 1. 딥러닝: 퍼셉트론과 다층 퍼셉트론 (0) | 2025.01.13 |