1. 선형 회귀 분석
* 선형 회귀 분석(Linear Regression)은 주어진 데이터에서 입력 변수(독립 변수)와 출력 변수(종속 변수) 사이의 관계를 직선(또는 다차원에서는 평면)으로 설명하고, 새로운 입력 값에 대한 출력을 예측하는 통계 및 머신러닝 기법입니다.
* 예를 들어, 공부 시간(입력 변수)과 시험 점수(출력 변수) 사이의 관계를 분석해 "공부 시간이 늘어날수록 시험 점수가 증가한다"는 패턴을 찾아냅니다.
* 이 과정에서 선형 회귀는 "Y = W X + b"라는 수식(기울기 W와 절편 b)으로 데이터를 표현하며, 최적의 기울기와 절편을 찾기 위해 비용 함수(Cost Function)를 최소화하는 경사 하강법(Gradient Descent) 등의 알고리즘을 사용합니다.
* 최종적으로 선형 회귀 모델은 주어진 입력 값에 대해 가장 적합한 예측 결과를 제공합니다.
2. 단항 선형 회귀
* 단항 선형 회귀(Simple Linear Regression)는 하나의 독립 변수(입력 변수, X)를 사용하여 하나의 종속 변수(출력 변수, Y)를 예측하는 통계 및 머신러닝 기법입니다.
* 입력 변수와 출력 변수 사이의 관계를 직선(Linear Line)으로 나타내며, 데이터의 패턴을 기반으로 가장 잘 맞는 직선을 찾아내어 새로운 입력 값에 대한 출력을 예측합니다.
1. 파이토치를 import 해줍니다.
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
2.
torch.manual_seed(2025)는 PyTorch의 난수 생성기의 시드를 고정합니다.
import torch
# torch.manual_seed(2025)는 PyTorch의 난수 생성기의 시드를 고정합니다.
# 이는 동일한 시드 값을 사용하여 실행할 때마다 동일한 난수를 생성하게 만듭니다.
# 이렇게 하면 코드의 재현성을 보장할 수 있습니다.
torch.manual_seed(2025)
예시 1)
import torch
# x_train과 y_train은 각각 입력 데이터와 출력 데이터를 나타냅니다.
# torch.FloatTensor는 32비트 부동소수점(float) 텐서를 생성합니다.
# x_train은 3x1 형태의 2차원 텐서로, 학습에 사용할 입력 값입니다.
# 값은 [[1], [2], [3]]로, 각 열이 하나의 샘플을 나타냅니다.
x_train = torch.FloatTensor([[1], [2], [3]])
# y_train은 3x1 형태의 2차원 텐서로, 학습에 사용할 출력 값입니다.
# 값은 [[2], [4], [6]]로, x_train과의 관계(단순한 선형 관계: y = 2x)를 표현합니다.
y_train = torch.FloatTensor([[2], [4], [6]])
# x_train 텐서와 y_train의 모양(shape)을 출력합니다.
print(x_train, x_train.shape)
-->
tensor([[1.],
[2.],
[3.]]) torch.Size([3, 1])
print(y_train, y_train.shape)
-->
tensor([[1.],
[2.],
[3.]]) torch.Size([3, 1])
예시 2)
import matplotlib.pyplot as plt
# figure() 함수는 새로운 그림(figure)을 생성합니다.
# figsize=(6, 4)는 생성된 그림의 크기를 설정합니다.
# 여기서 6은 가로 길이(인치 단위), 4는 세로 길이를 의미합니다.
plt.figure(figsize=(6, 4))
# scatter() 함수는 산점도를 그립니다.
# x_train은 x축 좌표, y_train은 y축 좌표 값입니다.
# 이 산점도는 x_train과 y_train 간의 관계를 시각적으로 나타냅니다.
plt.scatter(x_train, y_train)
-->
<matplotlib.collections.PathCollection at 0x7c95fbcfcb80>
시각적으로 데이터를 확인할 수 있는 그래프를 생성합니다.
그래프로 나타내면 학습 데이터(x_train, y_train)의 분포를 보여줍니다.
-->

예시 3)
import torch.nn as nn
# y = Wx + b
# 여기서 W는 가중치(weight), b는 편향(bias)을 의미합니다.
# nn.Linear는 선형 변환을 수행하는 신경망 계층입니다.
# nn.Linear(1, 1)은 입력 특성(input features)의 수가 1개이고,
# 출력 특성(output features)의 수도 1개인 선형 계층을 생성합니다.
# 즉, 이 계층은 y = Wx + b 형태의 선형 변환을 수행합니다.
model = nn.Linear(1, 1) # 입력 특성의 수, 출력 특성의 수
# 생성된 모델을 출력합니다.
# 모델 정보에는 계층의 종류와 해당 계층의 입력 및 출력 특성이 표시됩니다.
print(model)
-->
Linear(in_features=1, out_features=1, bias=True)
예시 4)
# y_pred = model(x_train)은 x_train 데이터를 선형 모델에 입력하여 예측 값을 계산합니다.
# 여기서 model은 nn.Linear로 정의된 선형 계층입니다.
# 모델은 학습 가능한 가중치(W)와 편향(b)을 사용하여 y_pred = Wx + b를 계산합니다.
# y_pred는 x_train에 대해 계산된 예측 값(predicted values)을 나타내는 텐서입니다.
# 아직 모델이 학습되지 않았으므로 초기 가중치와 편향 값에 따라 예측 결과가 출력됩니다.
y_pred = model(x_train)
print(y_pred)
-->
tensor([[-0.4630],
[ 0.0311],
[ 0.5252]], grad_fn=<AddmmBackward0>)
예시 5)
# model.parameters()는 모델의 학습 가능한 모든 파라미터(가중치와 편향)를 반환합니다.
# 여기서 model은 nn.Linear로 정의된 선형 모델입니다.
# nn.Linear의 경우, 학습 가능한 파라미터는 가중치(weight)와 편향(bias)입니다.
# 이 파라미터들은 초기에는 무작위로 설정되며, 학습 과정에서 업데이트됩니다.
# list()로 반환된 파라미터를 리스트 형태로 변환하여 출력합니다.
# #-0.4199*1 + -0.2018
print(list(model.parameters()))
-->
[Parameter containing:
tensor([[-0.4199]], requires_grad=True), Parameter containing:
tensor([-0.2018], requires_grad=True)]
>손실 함수
* 손실 함수(Loss Function)는 머신러닝과 딥러닝 모델이 예측한 값과 실제 값 사이의 차이를 수치적으로 나타내는 함수입니다.
* 모델이 학습을 통해 최적의 결과를 도출하려면 이 차이를 최소화해야 합니다.
* 손실 함수는 예측값과 실제값의 오차를 계산하여 하나의 숫자(스칼라 값)로 반환하며, 이 값은 비용(Cost) 또는 오차(Error)라고도 불립니다.
* 예를 들어, 회귀 문제에서는 주로 평균 제곱 오차(MSE, Mean Squared Error)를 사용하여 예측값과 실제값 간의 평균적인 차이를 측정하고, 분류 문제에서는 교차 엔트로피 손실(Cross-Entropy Loss)을 사용해 예측 확률 분포와 실제 레이블 분포 간의 차이를 계산합니다.
* 손실 함수가 반환한 값은 역전파(Backpropagation)를 통해 모델의 가중치와 편향을 조정하는 데 사용됩니다.
* 즉, 손실 함수는 모델이 학습 과정에서 목표로 삼아야 할 방향을 알려주는 나침반 역할을 합니다.
예시 1)
# (y_pred - y_train)는 모델의 예측 값(y_pred)과 실제 값(y_train) 간의 차이를 계산합니다.
# 이 차이는 각 데이터 포인트에 대한 예측 오차를 나타냅니다.
# 오차는 텐서로 반환됩니다.
# (y_pred - y_train)**2는 예측 오차의 제곱을 계산합니다.
# 제곱을 통해 음수 값을 모두 양수로 변환하여 오차의 크기를 강조합니다.
# 이는 평균 제곱 오차(Mean Squared Error, MSE)를 계산하기 위한 단계입니다.
# .mean()은 오차 제곱 값의 평균을 계산합니다.
# 이 값은 모델의 성능을 평가하는 손실(loss)로 사용됩니다.
# 손실 값이 작을수록 모델이 실제 데이터에 더 잘 맞는다는 것을 의미합니다.
loss = ((y_pred - y_train)**2).mean()
-->
tensor(17.2641, grad_fn=<MeanBackward0>)
예시 2)
import torch.nn as nn
# nn.MSELoss()는 PyTorch에서 제공하는 평균 제곱 오차(Mean Squared Error, MSE) 손실 함수입니다.
# MSE는 (y_pred - y_train)의 제곱의 평균을 계산하여 손실 값을 반환합니다.
# 이 손실 함수는 회귀 문제에서 자주 사용됩니다.
# mse_loss = nn.MSELoss()
# mse_loss(y_pred, y_train)은 모델의 예측 값(y_pred)과 실제 값(y_train)을 입력으로 받아
# 평균 제곱 오차(MSE) 손실 값을 계산합니다.
# 이 값은 모델이 얼마나 잘 예측했는지를 나타냅니다.
# mse_loss(y_pred, y_train)
# 또는 한 줄로 작성 가능합니다:
loss = nn.MSELoss()(y_pred, y_train)
print(loss)
-->
tensor(17.2641, grad_fn=<MseLossBackward0>)
> 최적화
* 최적화(Optimization)는 주어진 목표를 달성하기 위해 최상의 해결책(Optimal Solution)을 찾아가는 과정입니다.
* 머신러닝과 딥러닝에서는 주로 모델이 예측한 값과 실제 값 사이의 오차(손실 함수 값)를 최소화하는 것을 목표로 합니다.
* 이 과정에서 모델의 학습 가능한 파라미터(가중치와 편향)를 조정하여 손실 함수의 값을 점점 더 작게 만들어갑니다.
* 최적화는 주로 경사 하강법(Gradient Descent)과 같은 알고리즘을 사용해 수행되며, 손실 함수의 기울기(Gradient)를 따라가며 최저점(또는 최적점)을 찾습니다.
* 이 과정은 마치 산에서 가장 낮은 지점을 찾아 내려가는 것과 비슷합니다. 최적화는 단순히 손실을 줄이는 것뿐만 아니라, 학습 속도, 안정성, 과적합 방지와 같은 다양한 요소를 고려해야 하는 복합적인 과정입니다.
* 즉, 최적화는 모델이 데이터로부터 가장 정확하고 효율적인 예측을 할 수 있도록 파라미터를 조정하는 핵심 과정입니다.
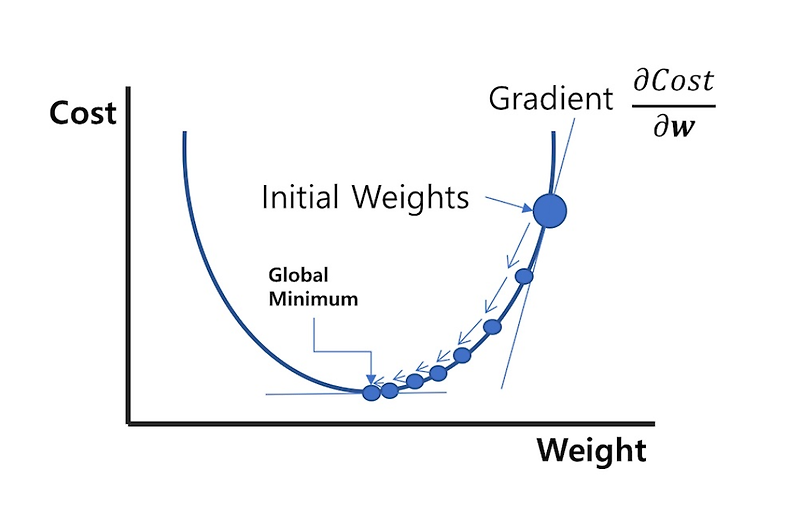
> 경사하강법
* 경사하강법(Gradient Descent)은 머신러닝과 딥러닝 모델이 최적의 가중치(Weights)와 편향(Biases)를 찾기 위해 손실 함수(Loss Function)를 최소화하는 방법입니다.
* 이 알고리즘은 마치 산 꼭대기에서 출발해 가장 낮은 지점(최솟값)을 찾아 내려가는 과정과 비슷합니다.
* 먼저, 모델은 손실 함수의 기울기(Gradient)를 계산합니다.
* 이 기울기는 현재 지점에서 손실이 가장 빠르게 감소하는 방향을 나타냅니다.
* 이후, 모델은 기울기의 반대 방향으로 가중치와 편향 값을 조금씩 업데이트합니다.
* 이때 학습률(Learning Rate)은 한 번에 이동하는 "걸음의 크기"를 결정합니다.
* 학습률이 너무 크면 최적의 지점을 지나칠 수 있고, 너무 작으면 학습 속도가 매우 느려질 수 있습니다.
* 이 과정을 반복하면서 손실 함수 값이 점점 작아지고, 결국 최적의 가중치와 편향을 찾아내게 됩니다.
* 즉, 경사하강법은 모델이 더 나은 예측을 할 수 있도록 가중치를 조정해주는 핵심 최적화 알고리즘입니다.
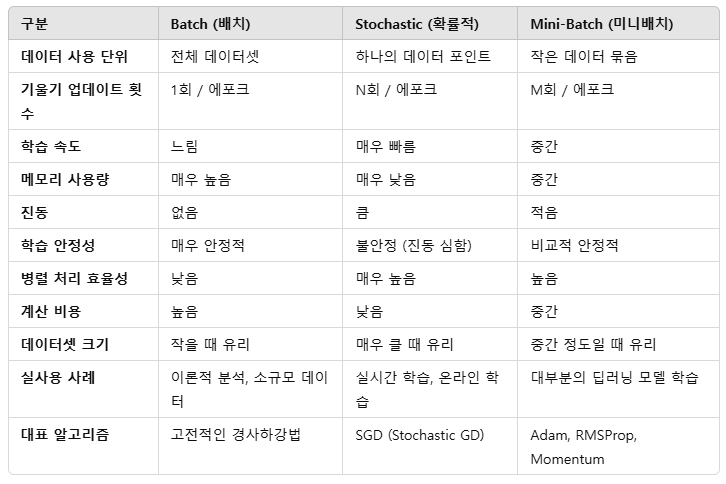
경사하강법은 데이터를 어떻게 나눠서 학습하느냐에 따라 배치(Batch), 확률적(Stochastic), 미니배치(Mini-Batch)로 나뉩니다.
> 학습률
* 학습률(Learning Rate)은 머신러닝과 딥러닝 모델이 학습할 때 가중치(Weights)와 편향(Biases)를 얼마나 크게 조정할지를 결정하는 하이퍼파라미터입니다.
* 경사하강법(Gradient Descent)과 같은 최적화 알고리즘에서 손실 함수(Loss Function)의 기울기(Gradient)를 따라 최적의 가중치를 찾아갈 때, 학습률은 한 번의 업데이트에서 이동하는 "걸음의 크기"를 의미합니다.
* 학습률이 너무 크면 최적의 가중치를 지나쳐 버리거나 학습이 불안정해질 수 있고, 너무 작으면 학습 속도가 매우 느려져 최적값에 도달하기 어려울 수 있습니다.
* 따라서 적절한 학습률을 선택하는 것은 모델의 학습 속도와 최적화 성능을 결정하는 중요한 요소입니다.
* 일반적으로 고정된 학습률을 사용하기도 하지만, 상황에 따라 학습률을 점진적으로 줄이거나 동적으로 조정하는 방법(예: Adam, Step Decay, Cyclical Learning Rate 등)이 사용되기도 합니다.
> 확률적 경사하강법
* SGD(Stochastic Gradient Descent, 확률적 경사하강법)는 모델의 가중치(Weights)와 편향(Biases)를 최적화하기 위해 손실 함수(Loss Function)의 기울기(Gradient)를 따라 반복적으로 업데이트하는 가장 기본적인 옵티마이저입니다.
* 일반적인 경사하강법은 전체 데이터셋을 한 번에 사용해 기울기를 계산하지만, SGD는 무작위로 선택된 하나의 데이터 포인트(순수 SGD) 또는 작은 그룹(미니배치 SGD)을 사용해 기울기를 계산하고 가중치를 조정합니다.
* 이로 인해 학습 속도가 빨라지고 메모리 사용량이 줄어들지만, 진동이 발생할 수 있어 학습이 불안정할 수도 있습니다.
* PyTorch에서 SGD는 optim.SGD로 구현되며, 학습률(lr)과 모멘텀(momentum) 등의 매개변수를 통해 조정할 수 있습니다.
* 주로 작은 데이터셋이나 빠른 반복 학습이 필요한 경우 사용되며, 학습률이 적절하게 설정되면 강력하고 효율적인 최적화 결과를 제공합니다.
예시 1)
import torch.optim as optim
# 1. 옵티마이저 정의
# optim.SGD는 확률적 경사 하강법(Stochastic Gradient Descent)을 사용하는 옵티마이저입니다.
# model.parameters()는 모델의 학습 가능한 파라미터(가중치 W와 편향 b)를 전달합니다.
# lr=0.01은 학습률(learning rate)을 설정하며, 학습률은 모델이 학습 중에 얼마나 빠르게 파라미터를 업데이트할지 결정합니다.
# 학습률은 데이터와 문제의 복잡도에 따라 다르게 설정될 수 있습니다.
optimizer = optim.SGD(model.parameters(), lr=0.01)
# 2. Gradient 초기화
# optimizer.zero_grad()는 이전 단계에서 계산된 기울기(gradient)를 0으로 초기화합니다.
# PyTorch는 기본적으로 역전파(backpropagation) 시 기울기를 누적(accumulate)하므로,
# 새로운 학습 단계에서 이전 단계의 기울기가 영향을 미치지 않도록 초기화가 필요합니다.
optimizer.zero_grad()
# 3. 손실 값에 대한 역전파
# loss.backward()는 손실(loss)을 기준으로 모델의 각 파라미터(W, b)에 대한 기울기(gradient)를 계산합니다.
# 역전파(backpropagation)는 손실 함수의 값을 줄이기 위해 각 파라미터가 얼마나 변화해야 하는지를 결정합니다.
loss.backward()
# 4. W와 b 업데이트
# optimizer.step()은 계산된 기울기(gradient)를 기반으로 모델의 파라미터(W, b)를 업데이트합니다.
# 학습률(lr=0.01)을 사용하여 기울기에 비례한 만큼 파라미터를 조정합니다.
optimizer.step()
#tensor([[0.6729]], requires_grad=True), Parameter containing:
#tensor([-0.8777], requires_grad=True)]
# 5. 업데이트된 모델 파라미터 확인
# list(model.parameters())는 업데이트된 모델의 가중치(W)와 편향(b)를 출력합니다.
# 결과는 Parameter 객체로 반환되며, 업데이트된 값이 반영됩니다.
print(list(model.parameters())) # W: 0.6729 , b: -0.8777
-->
[Parameter containing:
tensor([[0.6729]], requires_grad=True), Parameter containing:
tensor([-0.8777], requires_grad=True)]
예시 2)
epochs = 1000 # 총 학습 반복 횟수를 1000으로 설정합니다.
# for문을 사용하여 학습을 반복합니다.
# range(epochs + 1)는 0부터 epochs(1000)까지 총 100번 반복합니다.
# 1. 모델의 예측 값 계산
# x_train 데이터를 모델에 전달하여 예측 값(y_pred)을 계산합니다.
# 2. 손실 함수 계산
# nn.MSELoss()(y_pred, y_train)는 모델의 예측 값(y_pred)과 실제 값(y_train) 간의 평균 제곱 오차(MSE)를 계산합니다.
# 3. 기울기 초기화
# optimizer.zero_grad()는 이전 단계에서 계산된 기울기를 0으로 초기화합니다.
# 4. 역전파
# loss.backward()는 손실(loss)을 기준으로 모델의 각 파라미터(W, b)에 대한 기울기(gradient)를 계산합니다.
# 5. 파라미터 업데이트
# optimizer.step()은 계산된 기울기를 사용하여 모델의 가중치(W)와 편향(b)를 업데이트합니다.
# 6. 진행 상태 출력
# 매 100번의 epoch마다 현재 학습 단계(epoch)와 손실 값(loss)을 출력합니다.
# {epoch}/{epochs}는 현재 epoch와 총 epoch 수를 보여줍니다.
# {loss:.6f}는 손실 값을 소수점 6자리까지 출력합니다.
epochs = 1000
for epoch in range(epochs + 1): # for문을 사용하여 학습을 반복
y_pred = model(x_train) # x_train 데이터를 모델에 전달하여 예측 값(y_pred)을 계산
loss = nn.MSELoss()(y_pred, y_train) #nn.MSELoss()(y_pred, y_train)는 모델의 예측 값(y_pred)과 실제 값(y_train) 간의 평균 제곱 오차(MSE)를 계산
optimizer.zero_grad() # optimizer.zero_grad()는 이전 단계에서 계산된 기울기를 0으로 초기화
loss.backward() # loss.backward()는 손실(loss)을 기준으로 모델의 각 파라미터(W, b)에 대한 기울기(gradient)를 계산
optimizer.step() # optimizer.step()은 계산된 기울기를 사용하여 모델의 가중치(W)와 편향(b)를 업데이트
if epoch % 100 == 0: #매 100번의 epoch마다 현재 학습 단계(epoch)와 손실 값(loss)을 출력
print(f'Epoch: {epoch}/{epochs} Loss: {loss:.6f}')
-->
Epoch: 0/1000 Loss: 8.530635
Epoch: 100/1000 Loss: 0.005325
Epoch: 200/1000 Loss: 0.003291
Epoch: 300/1000 Loss: 0.002033
Epoch: 400/1000 Loss: 0.001257
Epoch: 500/1000 Loss: 0.000776
Epoch: 600/1000 Loss: 0.000480
Epoch: 700/1000 Loss: 0.000296
Epoch: 800/1000 Loss: 0.000183
Epoch: 900/1000 Loss: 0.000113
Epoch: 1000/1000 Loss: 0.000070
예시 3)
# 1. 모델의 최종 학습된 파라미터(W와 b)를 확인합니다.
# list(model.parameters())는 학습 완료 후 모델의 가중치(W)와 편향(b)를 반환합니다.
print(list(model.parameters()))
-->
[Parameter containing:
tensor([[2.0097]], requires_grad=True), Parameter containing:
tensor([-0.0220], requires_grad=True)]
# 학습된 모델의 식:
# y = 2.0097*x + -0.0220
# 위의 결과는 모델이 학습한 최종 선형 관계를 나타냅니다.
# x = 5일 때 y 값을 수동으로 계산:
result = 2.0097 * 5 + -0.0220 # 수식에 x=5를 대입하여 y를 계산합니다.
print(result) # 수동 계산한 y 값 출력
-->
10.0265
# 2. x_test 데이터를 생성합니다.
# torch.FloatTensor([[5]])는 입력 x 값으로 5를 가지는 2차원 텐서를 생성합니다.
x_test = torch.FloatTensor([[5]])
# 3. 모델에 x_test를 입력하여 예측 값을 계산합니다.
# model(x_test)는 학습된 모델에 x_test를 입력하여 y_pred를 계산합니다.
y_pred = model(x_test)
# 4. 모델의 예측 결과를 출력합니다.
# 학습된 파라미터(W, b)를 사용하여 y_pred를 계산하므로, 수동 계산 결과와 동일해야 합니다.
print(y_pred)
-->
tensor([[10.0264]], grad_fn=<AddmmBackward0>)
3. 다중 선형 회귀
* 다중 선형 회귀(Multiple Linear Regression)는 여러 개의 독립 변수(입력 변수)를 사용해 하나의 종속 변수(출력 변수)를 예측하는 통계 및 머신러닝 기법입니다.
* 단순 선형 회귀가 하나의 독립 변수와 하나의 종속 변수 간의 선형 관계를 설명하는 반면, 다중 선형 회귀는 두 개 이상의 입력 변수가 출력 변수에 어떻게 영향을 미치는지를 분석합니다.
* 이 관계는 수식으로 표현되며, 예를 들어 Y=W1X1+W2X2+...+WnXn+b와 같이 나타납니다.
* 여기서 Y는 예측 값, X1,X2,...Xn 은 입력 변수, W1,W2,...Wn 은 각 변수의 가중치, b는 절편입니다.
* 다중 선형 회귀는 입력 변수들이 독립적이고, 종속 변수와 선형 관계를 가진다는 가정 하에 작동하며, 주로 경제학, 의료, 마케팅 등 다양한 분야에서 복합적인 요인의 영향을 분석하고 예측하는 데 사용됩니다.
예시 1)
# torch.device는 PyTorch에서 사용 가능한 장치(CPU 또는 GPU)를 지정하는 데 사용된다.
# torch.cuda.is_available()는 현재 시스템에 GPU(CUDA 지원)가 사용 가능한지 확인한다.
# GPU가 사용 가능하면 'cuda'를 반환하고, 그렇지 않으면 'cpu'를 반환한다.
# 따라서 "cuda"를 사용할 수 있으면 GPU를, 그렇지 않으면 CPU를 사용하도록 설정한다.
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# 최종적으로 선택된 장치를 출력한다.
# GPU가 사용 가능하면 'device: cuda'가 출력되고, 그렇지 않으면 'device: cpu'가 출력된다.
print(f'device: {device}')
-->
device: cpu
예시 2)
# X_train은 학습에 사용할 입력 데이터로, 7개의 샘플(행)과 3개의 특징(열)으로 구성된 2D 텐서를 생성한다.
# torch.FloatTensor는 32비트 부동소수점(float) 데이터 타입의 텐서를 생성하는 함수이다.
# 각 행은 하나의 데이터 샘플이고, 각 열은 해당 샘플의 특징 값이다.
# .to(device)는 생성된 텐서를 지정된 장치(GPU 또는 CPU)로 이동시킨다.
X_train = torch.FloatTensor([[73, 80, 75], # 첫 번째 샘플의 특징 값
[93, 88, 93], # 두 번째 샘플의 특징 값
[89, 91, 90], # 세 번째 샘플의 특징 값
[96, 98, 100], # 네 번째 샘플의 특징 값
[73, 66, 70], # 다섯 번째 샘플의 특징 값
[85, 90, 88], # 여섯 번째 샘플의 특징 값
[78, 85, 82]]) # 일곱 번째 샘플의 특징 값
.to(device) # GPU 또는 CPU로 텐서를 이동
# y_train은 학습에 사용할 목표값(라벨)으로, 각 샘플에 해당하는 하나의 값(출력)을 가지는 2D 텐서를 생성한다.
# 각 행은 X_train의 각 샘플에 대응하는 출력 값이다.
# 마찬가지로, .to(device)는 이 텐서를 지정된 장치로 이동시킨다.
y_train = torch.FloatTensor([[152], # 첫 번째 샘플의 출력 값
[185], # 두 번째 샘플의 출력 값
[180], # 세 번째 샘플의 출력 값
[196], # 네 번째 샘플의 출력 값
[142], # 다섯 번째 샘플의 출력 값
[175], # 여섯 번째 샘플의 출력 값
[155]]) # 일곱 번째 샘플의 출력 값
.to(device) # GPU 또는 CPU로 텐서를 이동
# 생성된 X_train 텐서와 그 크기(shape)를 출력한다.
# X_train의 크기는 (7, 3)으로, 7개의 샘플과 각 샘플당 3개의 특징을 포함한다.
print(X_train, X_train.shape)
-->
tensor([[ 73., 80., 75.],
[ 93., 88., 93.],
[ 89., 91., 90.],
[ 96., 98., 100.],
[ 73., 66., 70.],
[ 85., 90., 88.],
[ 78., 85., 82.]]) torch.Size([7, 3])
# 생성된 y_train 텐서와 그 크기(shape)를 출력한다.
# y_train의 크기는 (7, 1)으로, 7개의 샘플과 각 샘플당 하나의 출력 값을 포함한다.
print(y_train, y_train.shape)
-->
tensor([[152.],
[185.],
[180.],
[196.],
[142.],
[175.],
[155.]]) torch.Size([7, 1])
예시 3)
# nn.Linear는 PyTorch에서 선형 변환(Linear Transformation)을 수행하는 신경망 층을 생성하는 클래스이다.
# 입력 차원(특징의 개수)과 출력 차원을 지정해야 한다.
# nn.Linear(3, 1)은 입력 차원이 3, 출력 차원이 1인 선형 변환 층을 생성한다.
# 즉, 입력 데이터가 3개의 특징을 가지면, 선형 결합을 통해 1개의 출력 값으로 변환된다.
# 내부적으로 nn.Linear는 가중치(weight)와 편향(bias)을 학습하도록 설정되어 있다.
# .to(device)는 생성된 모델을 지정된 장치(GPU 또는 CPU)로 이동시킨다.
model = nn.Linear(3, 1).to(device)
# 생성된 모델의 구조와 초기화된 가중치 및 편향 값을 출력한다.
# 출력은 nn.Linear 층에 대한 정보를 제공하며, 가중치와 편향은 초기화된 상태로 표시된다.
print(model)
-->
Linear(in_features=3, out_features=1, bias=True)
예시 4)
# optimizer = optim.SGD(model.parameters(), lr=0.00001)
optimizer = optim.Adam(model.parameters(), lr=0.01)
loss_fn = nn.MSELoss()
-->
# optimizer는 모델의 학습을 위해 사용되는 최적화 알고리즘을 설정한다.
# optim.Adam은 Adam(Adaptive Moment Estimation) 알고리즘을 사용하는 PyTorch의 최적화 클래스이다.
# model.parameters()는 모델의 학습 가능한 매개변수(가중치와 편향)를 반환하며,
# 이 매개변수들이 optimizer에 의해 업데이트된다.
# lr=0.01은 학습률(learning rate)을 지정하며, 매개변수 업데이트 시 변화량의 크기를 조정한다.
optimizer = optim.Adam(model.parameters(), lr=0.01)
# loss_fn은 손실 함수(loss function)를 정의한다.
# nn.MSELoss는 평균 제곱 오차(Mean Squared Error, MSE)를 계산하는 손실 함수이다.
# 이 손실 함수는 예측 값과 실제 값 간의 차이를 제곱하여 평균을 계산하며,
# 회귀 문제에서 자주 사용된다.
loss_fn = nn.MSELoss()
예시 5)
epochs = 1000
for epoch in range(epochs + 1):
y_pred = model(X_train)
loss = loss_fn(y_pred, y_train)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 100 == 0:
print(f'Epoch: {epoch}/{epochs}, Loss: {loss.item():.6f}')
-->
Epoch: 0/1000, Loss: 1367005184.000000
Epoch: 100/1000, Loss: 6.382938
Epoch: 200/1000, Loss: 6.345489
Epoch: 300/1000, Loss: 6.310021
Epoch: 400/1000, Loss: 6.276417
Epoch: 500/1000, Loss: 6.244575
Epoch: 600/1000, Loss: 6.214402
Epoch: 700/1000, Loss: 6.185805
Epoch: 800/1000, Loss: 6.158756
Epoch: 900/1000, Loss: 6.133082
Epoch: 1000/1000, Loss: 6.108780
# 학습을 반복할 횟수(epoch)를 설정한다.
# 1000번의 학습 반복을 수행한다.
epochs = 1000
# 학습을 1번부터 epochs+1번(즉, 1~1000번)까지 반복한다.
for epoch in range(epochs + 1):
# 1. 모델에 입력 데이터(X_train)를 전달하여 예측 값(y_pred)을 계산한다.
# model(X_train)은 X_train을 모델의 forward 함수(선형 변환)에 입력해 예측 결과를 반환한다.
y_pred = model(X_train)
# 2. 손실 함수(loss_fn)를 사용하여 예측 값(y_pred)과 실제 값(y_train) 간의 손실(loss)을 계산한다.
# MSELoss를 사용하므로, 예측 값과 실제 값의 차이를 제곱하여 평균을 계산한다.
loss = loss_fn(y_pred, y_train)
# 3. optimizer의 기울기(gradient)를 초기화한다.
# 이 작업은 이전 단계에서 계산된 기울기를 누적하지 않도록 한다.
optimizer.zero_grad()
# 4. loss.backward()를 호출하여 손실(loss)에 대한 모델 파라미터의 기울기를 계산한다.
# 이 과정은 역전파(backpropagation)라고 한다.
loss.backward()
# 5. optimizer.step()을 호출하여 계산된 기울기를 기반으로 모델 파라미터(가중치와 편향)를 업데이트한다.
optimizer.step()
# 6. 100번마다 현재 epoch과 손실 값을 출력한다.
# epoch과 총 epochs 중 진행 상태를 표시하고, 손실 값은 소수점 6자리까지 출력한다.
if epoch % 100 == 0:
print(f'Epoch: {epoch}/{epochs}, Loss: {loss.item():.6f}')
> Adam
* Adam(Adaptive Moment Estimation)은 경사하강법(Gradient Descent)을 개선한 최적화 알고리즘으로, 머신러닝과 딥러닝 모델 학습에서 널리 사용됩니다.
* Adam은 SGD(Stochastic Gradient Descent)의 단점을 보완하기 위해 개발되었으며, 각 가중치(Weight)와 편향(Bias)마다 다른 학습률(Learning Rate)을 적용해 더욱 효율적이고 안정적으로 최적화를 수행합니다.
* 이 알고리즘은 기울기의 평균(1차 모멘트, First Moment)과 기울기 제곱의 평균(2차 모멘트, Second Moment)을 모두 활용하여 학습률을 동적으로 조정합니다.
* 학습 초반에는 빠르게 학습하고, 학습 후반에는 안정적으로 수렴하도록 설계되었습니다. Adam은 계산 비용이 적고, 메모리 사용량이 효율적이며, 하이퍼파라미터를 따로 튜닝하지 않아도 대부분의 문제에서 좋은 성능을 보여줍니다.
예시 1)
list(model.parameters())
-->
# model.parameters()는 모델의 학습 가능한 파라미터(가중치와 편향)를 반환한다.
# nn.Linear의 경우, 학습 가능한 파라미터는 다음 두 가지이다:
# 1. 가중치(weight): 입력 특징의 각 값에 곱해지는 행렬 형태의 값
# 2. 편향(bias): 출력에 더해지는 상수 값
# list(model.parameters())는 이 파라미터들을 리스트 형태로 반환한다.
# 반환된 리스트의 첫 번째 요소는 가중치(weight) 텐서이고,
# 두 번째 요소는 편향(bias) 텐서이다.
# 예를 들어, nn.Linear(3, 1)의 경우:
# - 가중치(weight)의 크기는 (1, 3)으로, 입력 차원(3)과 출력 차원(1)에 따라 결정된다.
# - 편향(bias)의 크기는 (1,)으로, 출력 차원에 해당한다.
list(model.parameters())
-->
[Parameter containing:
tensor([[1.1905, 0.4599, 0.3552]], requires_grad=True),
Parameter containing:
tensor([-0.1236], requires_grad=True)]
예시 2)
# y = 1.1905 * x1 + 0.4599 * x2 + 0.3552 * x3 + -0.1236
x_test = torch.FloatTensor([[93, 93, 93]]).to(device)
print(1.1905*93 + 0.4599*93 + 0.3552*93 + -0.1236)
y_pred = model(x_test)
print(y_pred)
-->
186.3972
tensor([[186.3932]], grad_fn=<AddmmBackward0>)
# 모델이 학습한 가중치와 편향 값을 기반으로 예측 값을 계산하는 예제이다.
# 학습된 모델의 예측 식(y = 1.1905 * x1 + 0.4599 * x2 + 0.3552 * x3 + -0.1236)을 사용한다.
# x1, x2, x3는 각각 입력 데이터의 특징 값이다.
# 테스트 데이터를 생성한다. x_test는 [93, 93, 93]으로 구성된 2D 텐서이다.
# to(device)는 이 데이터를 모델과 동일한 장치(GPU 또는 CPU)로 이동시킨다.
x_test = torch.FloatTensor([[93, 93, 93]]).to(device)
# 학습된 가중치와 편향을 사용하여 수동으로 예측 값을 계산한다.
# 각각 x1=93, x2=93, x3=93를 대입하고, 수식을 직접 계산한다.
print(1.1905 * 93 + 0.4599 * 93 + 0.3552 * 93 + -0.1236)
# 모델을 사용하여 x_test에 대한 예측 값을 계산한다.
# model(x_test)는 x_test를 모델의 forward 함수에 전달하여 예측 값을 계산한다.
# 이 결과는 학습된 가중치와 편향을 사용하여 자동으로 계산된다.
y_pred = model(x_test)
# 모델을 사용한 예측 값을 출력한다.
# y_pred는 모델이 학습된 파라미터를 사용하여 계산한 결과로,
# 앞서 직접 계산한 값과 유사한 값이 출력된다.
print(y_pred)'LLM(Large Language Model)의 기초 > 데이터 분석' 카테고리의 다른 글
| 12. 주택 임대료 예측 데이터셋 (0) | 2025.01.07 |
|---|---|
| 11. 사이킷런 (0) | 2025.01.07 |
| 9. 파이토치 프레임워크 (2) | 2025.01.06 |
| 8. 머신러닝과 딥러닝 (2) | 2025.01.06 |
| 7. 커피프랜차이즈 이점 전략 (2) | 2024.12.23 |